前言
Games103 介绍了一种 Impulse Method 来响应。通过模拟冲量(Impulse)的方法响应刚体碰撞。本文将会进行较为详细的介绍。本文记
为
SDF 函数,记
SDF 函数梯度为 .
Impulse Method 并不是完全基于物理的,其做出了一定的假设,即动量是及时改变的,这意味着在碰撞响应的时候就计算物体相对应的动量衰减以及方向改变。而这部分
Penatly Method 处理得更好,可由于
Penatly 涉及到积分运算,也就是显式计算/隐式计算的问题,不易于计算机实现,因此不在讨论;而且
Penatly 的延时处理导致模拟程序要求的时间片段非常短,相对而言可能性能要求较高。
1. 利用 SDF 判断物体碰撞
利用 SDF 判断碰撞有两个方法,一个是对物体边缘上的每个点都进行一次
SDF 计算。这并在性能上并不划算,这里我将提供一种更好的方法,尽管这种方法可能会失去一些普适性,但是带来的性能证明这是值得的。
我们先考虑两个圆的碰撞如下图所示:
当两个圆还没相撞时,我们能观察到两个圆心之间的距离
满足 . 而又如下图,当两个圆已经发生了碰撞甚至重叠在一起时,如下图。
我们可以观察到两个圆心之间的距离 则满足 . 对应成 SDF
即为 .
因此,当
是,两圆相撞.
圆形搞定了,再来看圆和线之间的碰撞,如下图:
其实点与线之间的碰撞更为简单。只要
即可.
有了上述基础上,我们就可以描述了圆形与任意几何体(圆弧除外)之间的碰撞了,而线与线之间的碰撞由于篇幅原因,本文不再介绍,读者可自行介绍,我也并没有在代码中实现线线碰撞.
2. 碰撞后位置的修正
当两个物体碰撞以后,我们并不能确保物体的位置一定是在我们预期之中的,例如图
1.1 就是一个意外情况.由于速度过快导致两个物体出现了重叠。此时我们就需要修正物体的位置。现在我们关注如下图的情况.
难发现,我们所需要的位置修复就是将圆形沿着法线方向()移动两个圆之间的距离,也就是
.即
.
这里特地说一下 SDF 的梯度 在代码中如何求。对于圆形,我们可以直接求
,即对
求偏导.
而对于直线的 SDF,其
SDF 函数并不是很好写成数学表达式,就算写出来了其偏导产物也非常恐怖(我并没有尝试去这么做,如果尝试了然后发现其形式很优雅欢迎你在评论区指正).所以我们直接采用偏导的定义,即对
SDF 函数取一个很小的增量然后相减:
1
2
3
4
5
| auto GradientSDF(const Vec &Point) -> Vec override {
auto origin = SDF(Vec({Point.x[0], Point.x[1]}));
return Vec({SDF(Vec({Point.x[0] + 0.0000000001, Point.x[1]})) - origin,
SDF(Vec({Point.x[0], Point.x[1] + 0.0000000001})) - origin});
}
|
3. 碰撞后的速度修正
在进行速度的修正之前,我们应该确保一件事情:速度是需要修正的。什么意思呢,就是这个物体的速度可能已经在前几个
Tick 内被修正了,这种情况下我们就不需要在进行修正了.判断速度是否需要被修正的一个方法就是看其是否指向碰撞目标物体内,即比较
与 的大小. 若 ,则说明速度只向物体内部.
对于速度的修复,我们先将速度沿法相法相正交分解:. 然后分别进行速度更新,对于竖直方向的速度,有
. 其中
为法线方向上的弹性系数,需要手动设置; 为切方向上的摩擦系数,需要我们去算出来.
根据阿蒙顿-库仑摩擦定律(Amontons-Coulomb
Friction Laws),即“摩擦力与法向载荷成正比、摩擦因数与接触面积无关、摩擦因数与滑动速度无关、静摩擦因数大于动摩擦因数”.
我们可以得到式:
其中
为平面摩擦系数,需要自行设定.
然后代入整理解得:
在实际程序中,我们可以直接取该不等式等号。为了防止出现
超出我们所预期的范围 ,我们应该对其进行限制,即
.
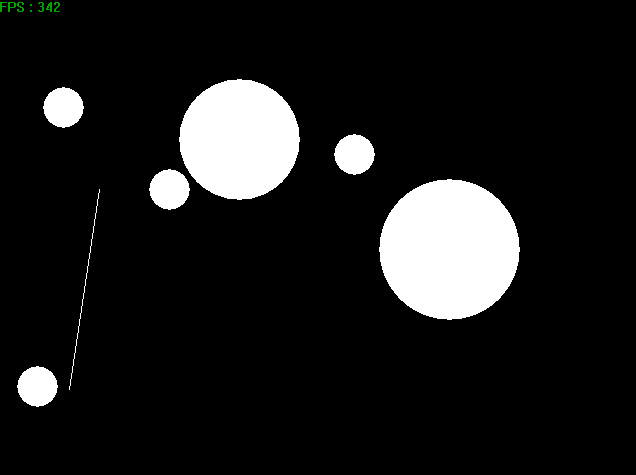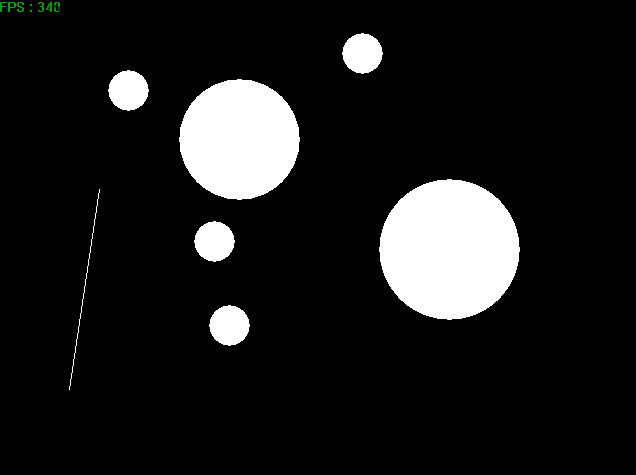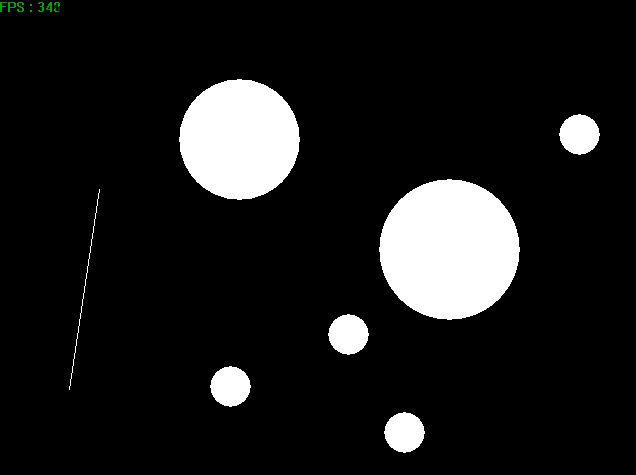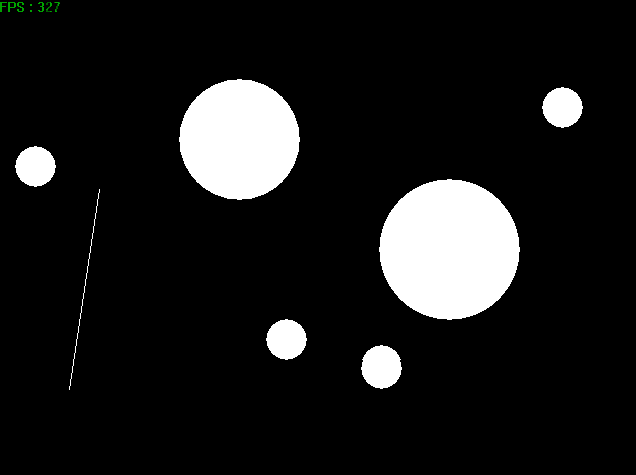
4. 结果展示
我没有进行动量衰减计算,我觉得这更利于展示。
ㄟ( ▔, ▔ )ㄏ